Abstract
This document provides a simple introduction to the current state of development of polynomial commitments and the application of hash functions in zero-knowledge proofs (zk). We conduct a detailed study and comparison of the two generations of Poseidon hash functions used in Plonky2 and Plonky3, and present benchmark results to verify the computational performance of Poseidon2.
Keywords: Plonky3; Polynomial Commitment; Hash; Poseidon2
Introduction
To ensure the data integrity of systems, most zero-knowledge proofs currently utilize polynomial commitment schemes. These schemes primarily function to:
Data Integrity Verification: Polynomial commitments can be used to commit to certain data, ensuring that the data is not tampered with during transmission or storage. The recipient can verify the integrity of the data by checking whether the commitment is correct.
Data Concealment: Polynomial commitments allow for the concealment of certain data without the need to disclose the actual data. Only those who know the corresponding commitment value can access the actual data.
Proof System Construction: In some zero-knowledge proof systems, it is necessary to demonstrate the existence or properties of a value within a polynomial. Polynomial commitments can be used to commit to values within a polynomial and verify these values during the proof process.
Random Number Generation: Polynomial commitments can be used to generate random numbers, ensuring their unpredictability and randomness. This is essential in some zero-knowledge proof systems, such as in cryptographic protocols where secure random numbers are generated.
Privacy Protection: Polynomial commitments help protect data privacy, as only individuals who know the corresponding commitment value can access the actual data, while others cannot discern the content of the actual data.
There are various methods of polynomial commitments, such as directly committing polynomial coefficients, which ensures that the polynomial cannot be altered post-commitment. However, when there are many coefficients, the commitment result can be large, increasing storage and transmission costs and not meeting the simplicity requirements of zero-knowledge proof systems. Therefore, current zero-knowledge proof systems employ point value commitment schemes, with common types including:
Pedersen Commitment: Introduced in 1992 [1], Pedersen Commitment is used mainly with elliptic curve cryptography (though it can also combine with exponential operations). It relies on the discrete logarithm assumption, mixing polynomial coefficients with random values to generate commitments and using the properties of discrete logarithms for concealment and integrity verification. Pedersen Commitment is primarily used in privacy-focused cryptocurrencies like Zcash, MimbleWimble, Monero, etc.
IPA Commitment [2]: Strictly speaking, the Inner Product Argument (IPA) is a technique for verifying whether the inner product of two vectors satisfies certain properties. It allows the prover to commit to a polynomial while providing evidence that the polynomial meets specific characteristics, such as having a zero inner product with another vector. During the proof process, the prover can use IPA polynomial commitments to conceal specific coefficients of the polynomial while ensuring the correctness and integrity of the proof.
KZG Commitment: A more efficient polynomial commitment scheme based on range proofs. It features quick generation and verification, suitable for applications requiring high efficiency. Systems using KZG Commitment include Groth16, Sonic, and StarkWare.
BCH Commitment: The BCH (Benaloh-Cohen-Horvitz) Commitment is a non-interactive polynomial commitment scheme allowing for verification without further interaction after the commitment is generated. It uses homomorphic properties, specifically log homomorphism and power homomorphism, allowing commitment verification through a single exponentiation and logarithm calculation, thus avoiding the need to verify each polynomial coefficient individually. This characteristic gives BCH Commitment advantages in specific zero-knowledge proof systems.
Fiat-Shamir Commitment: Based on the Fiat-Shamir transformation, this is a Merkle tree commitment scheme that converts interactive zero-knowledge proof protocols into a non-interactive form. In Fiat-Shamir Commitment, the committer can generate and verify commitments without interaction with the verifier, achieving a non-interactive nature. It can be combined with other polynomial commitment schemes to implement non-interactive zero-knowledge proof systems.
FRI Commitment: The FRI (Fast Reed-Solomon Interactive) Commitment is a scheme based on Reed-Solomon codes (a subset of BCH codes), used to build efficient zero-knowledge proof systems. Its advantage is that the size of the commitment scales linearly with the degree of the polynomial and can be effectively verified. However, FRI Commitment schemes require a trusted setup, which may be a drawback in some applications.
In various polynomial commitment schemes, those based on pair-based cryptography or Reed-Solomon codes are theoretically more secure due to stronger underlying assumptions, such as Pedersen and KZG commitments. Conversely, using Merkle trees for polynomial commitments, which rely on hash functions, has the advantage of simplicity and effective implementation. However, the security of Merkle-based schemes typically depends on the random oracle model, which does not exist in the real world, thus creating some security controversies.
Polynomial Commitment in Plonky
Plonky originated from zk-SNARKs proof systems, initially using the KZG commitment scheme employed by Plonky1, which gave Plonky1 a timing advantage. However, it was not truly computing recursive proofs but rather verifying them. A significant innovation in Plonky2 was the use of STARKs underlying protocol - the FRI commitment scheme, which does not involve any elliptic curves and uses hashing algorithms for polynomial commitment and verification processes. This is due to two essential features of hashes: first, hash calculations are generally fast, and second, they are defined in one domain, so the input and output of a hash are a series of field elements in the same domain. Thus, the proof system can use a small field (Goldilocks field) to complete fast proofs. Additionally, the FRI polynomial commitment has an important advantage in that it is entirely recursive, with complete recursive proofs available at any time for previous chains or trees, making it very simple in engineering terms, as the complete verifier is implemented in the circuit.
In contrast, Binius uses another new commitment scheme based on Brakedown (using Merkle trees and Reed-Solomon encoding). Compared to FRI, this scheme has larger proofs and longer verification times, but the Prover time can be significantly reduced.
Plonky3 is still in development, but it has already shown significant performance improvements over Plonky2. Plonky3 continues to use the FRI polynomial commitment scheme and has added the Brakedown commitment scheme. It has made improvements in the FRI implementation details, including using optimized data structures to store and operate the data required by the FRI protocol, using parallel computing to further enhance the efficiency of the FRI protocol, and using friendlier hash functions and smaller fields (Mersenne31 prime field).
Hash Function in ZK
In cryptography, hash functions are functions that map data of arbitrary size to a fixed-size output, known as the hash value or hash code. Hash functions have one-way and collision-resistant properties. Common hash functions include MD5, SHA-1, SHA-256, and SHA-3. For example, to verify the integrity of a file, you can use a hash function to compute the hash value of the file, then compare it with the expected hash value of the file. If the two hash values match, you can be confident that the file has not been tampered with.
In the field of zero-knowledge proofs, using collision-resistant hash functions can effectively eliminate the need for trusted setups or elliptic curve operations, making hash functions an indispensable part of zero-knowledge proof systems. The development of hash functions in zero-knowledge proof systems can be summarized in the following stages:
Stage One: General Hash Functions
In the early stages of zero-knowledge proofs, general hash functions, such as SHA-256 and MD5, were primarily used. These hash functions were designed for various applications, including digital signatures and message authentication. However, they are not necessarily suitable for the specific needs of zero-knowledge proof systems.
Stage Two: Merkle Tree-based Commitment Schemes
As zero-knowledge proof technology evolved, many zero-knowledge proof systems began to develop specialized hash functions for zero-knowledge proofs. A significant marker is the use of Merkle tree-based commitment schemes. Merkle trees are binary trees constructed using hash functions. They can be used to build polynomial commitments, with the commitment value being the root hash value of the Merkle tree. The advantages of Merkle tree-based commitment schemes are their simplicity and effective implementation. However, the security of these schemes typically depends on the random oracle model, which does not exist in the real world, thus creating some theoretical security controversies.
Stage Three: Specialized Hash Functions
With the emergence and development of more efficient polynomial commitment schemes, specialized hash functions for zero-knowledge proofs have appeared, such as Poseidon[7] and Rescue-Prime[8]. These specialized hash functions are optimized for the specific needs of zero-knowledge proof systems, such as efficient computation and resistance to specific types of attacks.
In Plonky2, the Poseidon hash function is used as the node generation method for polynomial commitments. Poseidon uses a sponge/squeeze structure, absorbing everything and generating a fixed-size output. It features an internal state:
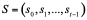
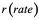
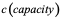
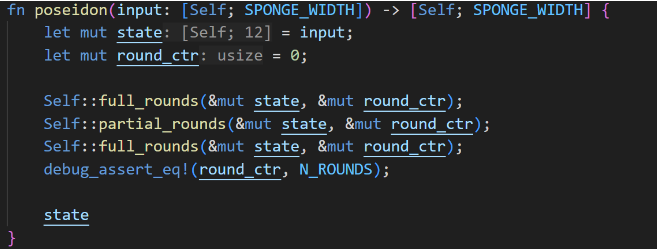
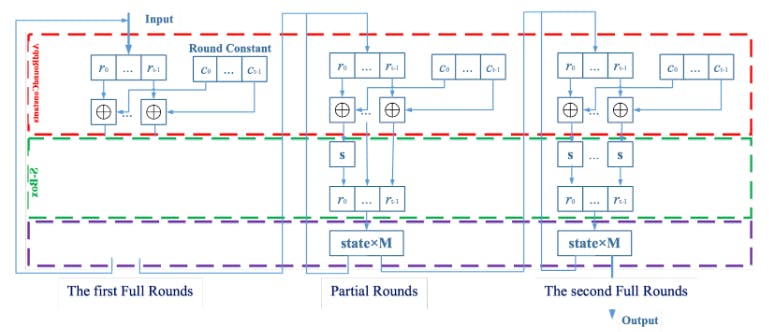
The Poseidon hash calculation mainly includes three steps: the first Full Rounds, Partial Rounds, and the second Full Rounds. The specific process is as follows.
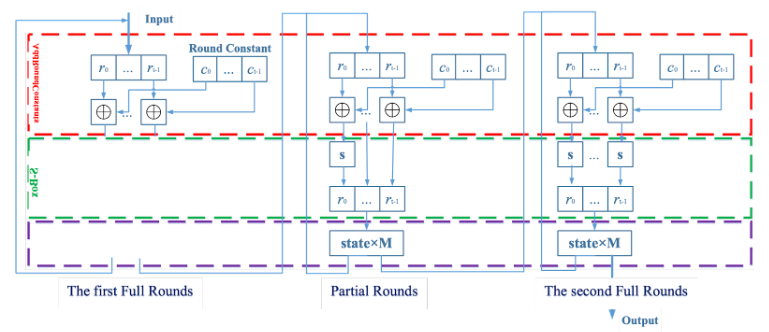
In the Full Rounds, each cycle requires sequentially completing the Add Round Constant, S-Box, and MDS Mixing (The Linear Layer/MixLayer) operations for all elements of the state vector. Add Round Constants require a single constant addition, S-Box requires calculating a seventh power modulus, and MDS Mixing involves multiplying the state vector by the constant matrix M.
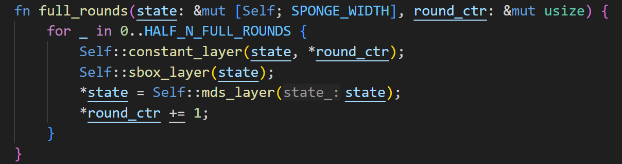
The calculation process for Partial Rounds and Full Rounds is essentially the same, with the difference being that in the S-Box stage of Partial Rounds, only the first element's modulus power calculation is needed.
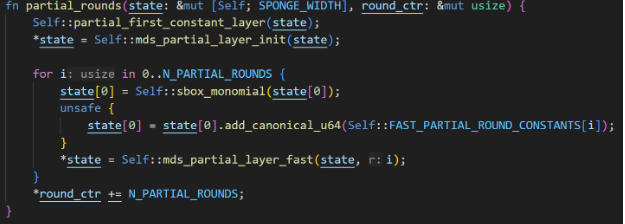
In Plonky2, Poseidon has 12 state inputs, with 3 Rounds, each Round executing 30 times, for a total of 90 Rounds. The simplified Poseidon calculation process is as follows.
![Figure 5: The Poseidon Construction in [7]](https://cdn.hackernoon.com/images/Ns6mVt8NqgNkfsouVyus9tAe3mB2-inc3401.png)
The Poseidon hash function is specifically developed based on the Goldilocks field, aiming to reduce the computational complexity for provers and verifiers in zero-knowledge proof systems. Compared to the Keccak hash function, there is no need to use a large circuit representation (Keccak introduces a lot of complexity in constraint design), hence Poseidon exhibits good computational performance in Plonky2.
Poseidon2 in Plonky3
Plonky3, compared to Plonky2, is more like a toolkit for building zero-knowledge-proof systems. Its open-source code includes many new features, several of which are important:
- Addition of the BabyBear domain used by the RISC Zero project:
And the faster Mersenne31 prime field:
[9]
- Addition of Brakedown encoding on top of the existing Reed-Solomon encoding[10].
- Implementation of faster circle FFT for the Mersenne31 prime field.
- A richer set of hash functions, including the newly added Rescue, Poseidon2, Monolith, along with the original Poseidon, Blake3, and Keccak, now totaling six hash functions.
These changes indicate the critical role of hash functions in the Plonky3 toolkit. This section focuses on analyzing the Poseidon2 hash function.
In 2023, Lorenzo Grassi and others improved the Poseidon hash function, introducing Poseidon2[11].
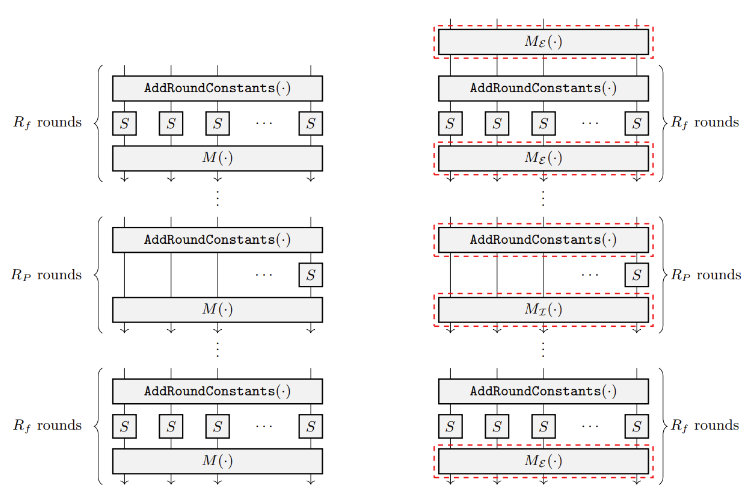
The main improvements (as shown in Figure 6) include:
- A linear layer
is applied at the input of Poseidon2;
- Two different linear layers with
and
are used in Poseidon2 for t ≥ 4.;
- Only one round constant is applied in each internal round;
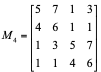
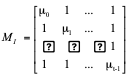
Plonky3 has optimizations for t ≥ 4, referencing the implementation of [12], with the core code as follows (Galois field, width=12). The red box in the figure shows the improved content.
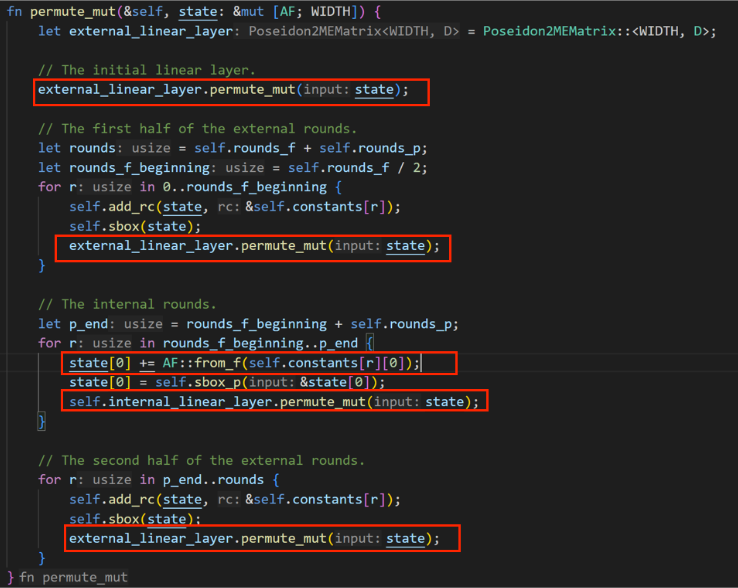
The linear layer has two constant matrices: 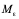
The advantages of the constant matrices are that we can compute the multiplication of 4 input elements by using only additions (a total of t-1 additions).
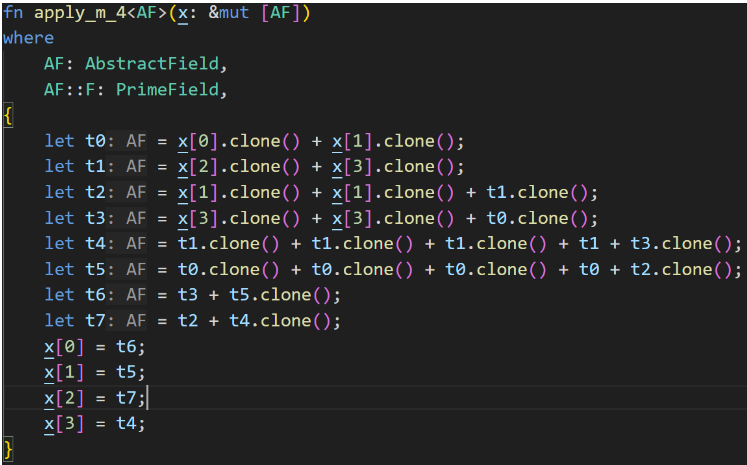
The second matrix is constructed as:
where 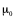
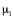
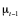
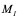
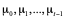
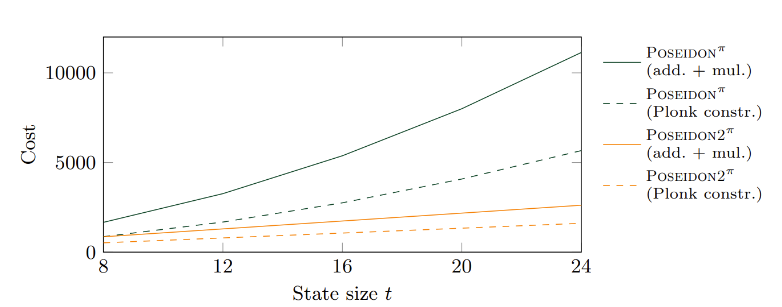
In summary, the improved Poseidon2 hash is simpler and uses less memory than Poseidon. As shown in the figure below, the number of operations and Plonk constraints needed for the linear layers in Poseidon2 is less than that in Poseidon.
Benchmarks of Poseidon2
We tested the performance of Poseidon2. The test code reference is [13]. The rust code focuses only on primitives without any high-degree components. The testing platform is as follows.
Operating System: Ubuntu22.04 CPU: Intel i7-13700H 2.40 GHz Memory: 64.0 GB DDR5 4800
In the benchmarks, we focus on two different primes used in Plonky3, namely the 64-bit Goldilocks and the 31-bit Babybear. The results are shown in Table 1. We can see that Poseidon2 has a significant performance improvement over Poseidon. Additionally, the advantage increases for larger state sizes, due to the expensive matrix multiplication in the external rounds of Poseidon.

References:
- Pedersen, T. (1992). "Non-interactive and information-theoretic secure verifiable secret sharing." Advances in Cryptology—CRYPTO'91. Springer Berlin Heidelberg..
- Groth, J., & Sahai, A. (2008, July). Efficient non-interactive proof systems for bilinear groups. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 415-432). Springer, Berlin, Heidelberg.
- Kate, A., Zaverucha, G. M., & Goldberg, I. (2010, May). Constant-size commitments to polynomials and their applications. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 177-194). Springer, Berlin, Heidelberg.
- .Benaloh, J., Cohen, N., & Horvitz, S. (1988). Multi-Exponentiation Cryptosystems. In CRYPTO'88 Proceedings of the 8th Annual International Cryptology Conference on Advances in Cryptology (pp. 195-210). Springer-Verlag.
- Fiat, A., & Shamir, A. (1986). How to prove yourself: Practical solutions to identification and signature problems. In Conference on the theory and application of cryptographic techniques (pp. 186-194). Springer, Berlin, Heidelberg.
- Fiat, A., & Shamir, A. (1986). How to prove yourself: Practical solutions to identification and signature problems. In Conference on the theory and application of cryptographic techniques (pp. 186-194). Springer, Berlin, Heidelberg.
- Lorenzo Grassi, Dmitry Khovratovich, Christian Rechberger, et al. POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems.
<https://eprint.iacr.org/2019/458.pdf](https://eprint.iacr.org/2019/458.pdf) . 2019. - Alan Szepieniec1 , Tomer Ashur2,3 , and Siemen Dhooghe. Rescue-Prime: a Standard Specification (SoK).
https://eprint.iacr.org/2020/1143.pdf. 2020 . - Ulrich Habock, Daniel Lubarov, Jacqueline Nabaglo. Reed-Solomon codes over the circle group.
https://eprint.iacr.org/2023/824.pdf. 2023 . - Alexander Golovnev, Jonathan Lee, Srinath Setty,et al. Brakedown: Linear-time and field-agnostic SNARKs for R1CS.
https://eprint.iacr.org/2021/1043.pdf. 2021 . - Lorenzo Grassi, Dmitry Khovratovich, and Markus Schofnegger. Poseidon2: A Faster Version of the Poseidon Hash Function.
323.pdf (iacr.org) . 2023. https://github.com/HorizenLabs/poseidon2/blob/main/plain_implementations/src/poseidon2/poseidon2_instance_goldilocks.rs GitHub - HorizenLabs/poseidon2