Authors:
(1) Agustin Moreno;
(2) Francesco Ruscelli.
Table of Links
- Abstract
- Introduction
- Preliminaries
- The B-signature
- GIT sequence: low dimensions
- GIT sequence: arbitrary dimension
- Appendix A. Stability, the Krein–Moser theorem, and refinements and References
4. GIT sequence: low dimensions
We now discuss global topological methods in the study of periodic orbits, following the exposition in [AFKM]. These methods encode: bifurcations; stability; eigenvalue configurations; obstructions to existence of regular families; and B-signs, in a visual and resource-efficient way.

The GIT sequence is the sequence of maps and spaces given by

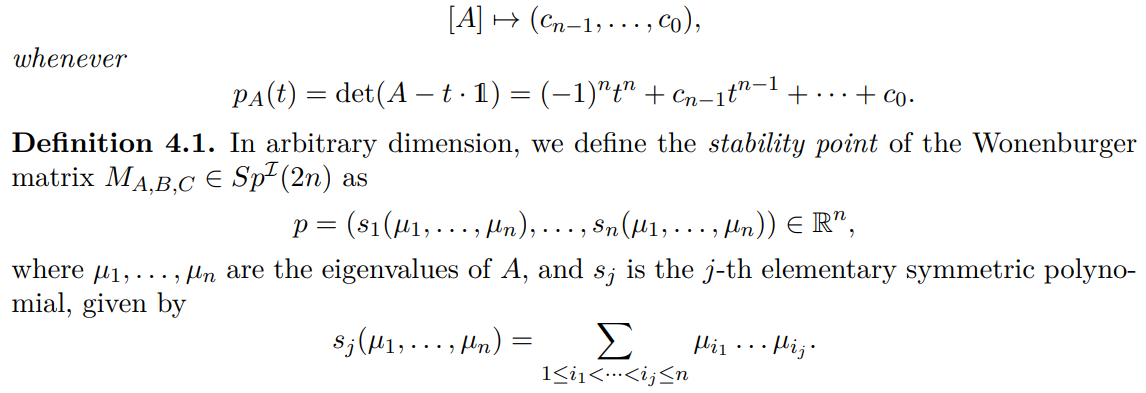
Then, by the above, the stability point is the result of applying the GIT sequence of maps to the given matrix.
4.1. GIT sequence: 2D. We start with the simplest case, i.e. the case of an autonomous Hamiltonian of two degrees of freedom, so that the reduced monodromy matrix is an element in Sp(2) = SL(2, R).
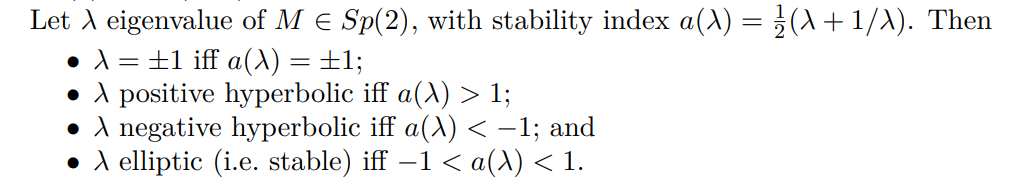
The Broucke stability diagram is then simply the real line, split into three components; see Figure 1. If two orbits lie in different components of the diagram, then there are always bifurcations in any family joining them, as the topology of the diagram implies that any path between them has to cross the ±1 eigenvalues (corresponding respectively to bifurcation or period-doubling bifurcation).
One can think that the stability index “collapses” the two elliptic branches in the middle layer of Figure 1 together. These two branches are distinguished by the B-signs, coinciding with the Krein signs [Kre2; Kre3]. There is an extra top layer for symmetric orbits, where now each hyperbolic branch separates into two, and there is a collapsing map from the top to middle layer. Note that to go from one branch to the other (say from the positive hyperbolic branch I to the positive hyperbolic branch II), the topology of the top layer implies that the eigenvalue 1 needs to be crossed. This means that one should expect bifurcations in any (symmetric) family joining them, even if they project to the same component of the Broucke diagram. In this way, the information given by the diagram is much more refined for the case of symmetric orbits. If we say that two orbits are qualitatively equivalent if they can be joined by a regular orbit cylinder, then the topology of the spaces in the GIT sequence give criteria to determine whenever two orbits are not qualitatively equivalent. To sum up:
• B-signs “separate” hyperbolic branches, for symmetric orbits.
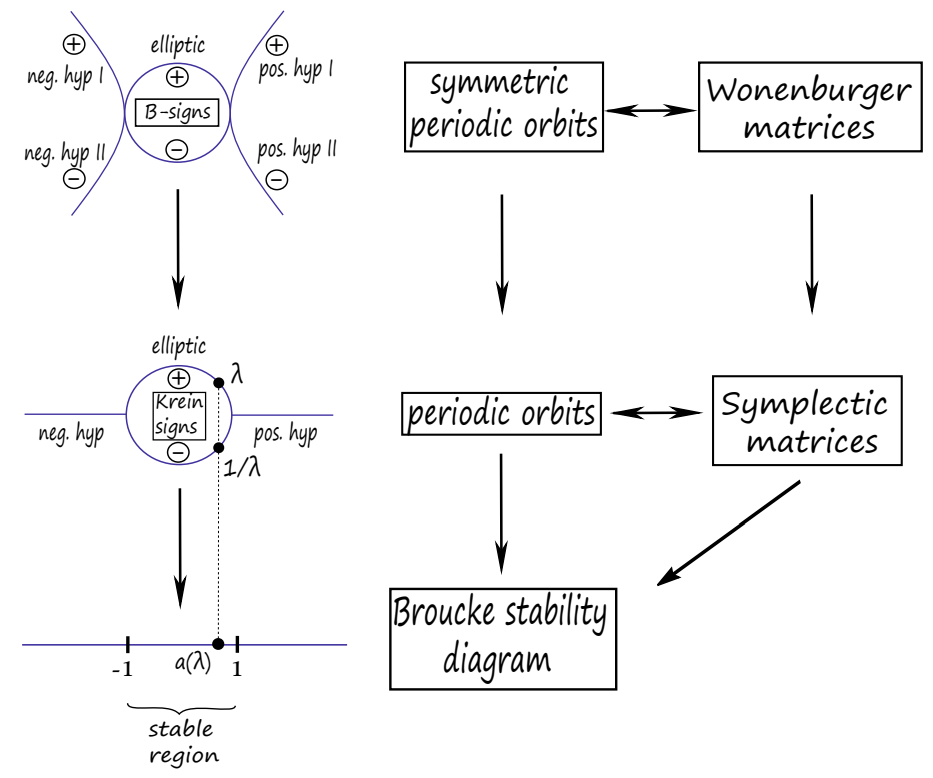
• If two orbits lie in different components of the Broucke diagram, there are always bifurcations in any path joining them.
• If two symmetric orbits lie in the same component of the Broucke diagram, but if B-signs differ, one should also expect bifurcation in any (symmetric) path joining them[1].
4.2. GIT sequence: 3D. Now we apply the same idea, but for autonomous Hamiltonian systems with three degrees of freedom, for which reduced monodromy matrices are elements in Sp(4).
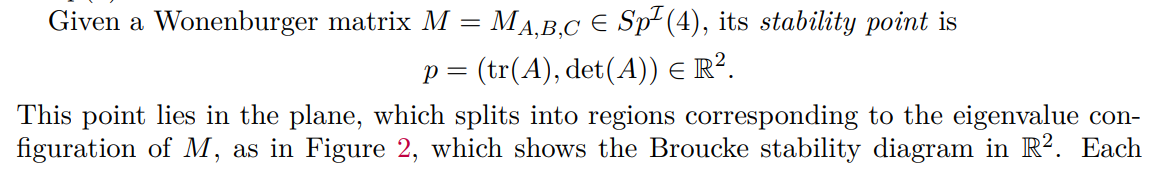
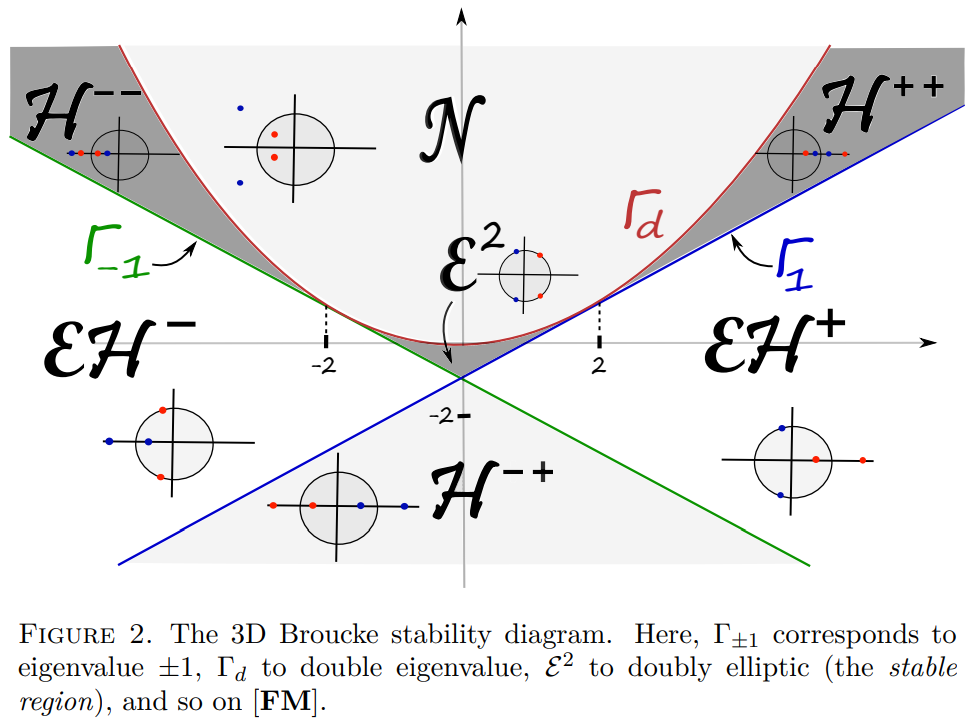

The GIT sequence [FM] adds two layers to this diagram, as shown in Figure 3. The top layer has two extra branches than the middle one, for each hyperbolic eigenvalue. While the combinatorics and the global topology of the spaces involved is more complicated than the 2D case, the intuitive idea is still the same, i.e. that the amount of information for symmetric orbits is richer, and that we can distinguish more orbits up to qualitative equivalence. Note that as in this dimension we have two pairs of eigenvalues, the B-signature is a pair (±, ±) of signs, and therefore the top layer has 4 branches over each component of the Broucke diagram (except the nonreal component).

This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
[1] We cautiosuly use the word “expect” rather than give a mathematical statement, as theoretically orbits could tangentially pass through the Maslov cycle without birfurcating.