An investment portfolio is a collection of financial assets, such as stocks, bonds, or cryptocurrency, in which an individual invests. An investment is mostly identified by its risk (how volatile the value is) and its return (what is the expected gain). Investors aim to build a portfolio that minimizes risk while maximizing return.
Since investments are all about understanding the numbers, expert traders utilize data science techniques and models to optimize their investment strategy. One such model is the Modern Portfolio Theory (MPT), also known as the Markowitz Mean-Variance Theory. The model provides the optimal investment portfolio using risk assessment and maximizes return for the investor.
Let’s understand the role of data science in making efficient investments, look at modern portfolio theory in detail, and discuss the assumptions and risks associated with data science models.
More On The Markowitz Mean-Variance Theory
The Markowitz Mean-Variance Theory was first published by Harry Markowitz in 1952. The theory presents a data-based model that analyzes financial trends to estimate risk and return. As a rule of thumb, investments are categorized as low-risk, low-return, and high-risk, high-return. In simpler terms, it establishes that investments with a higher risk factor carry a higher reward and vice versa.
MPT provides an optimal selection of investments that balances out risk for reward. The final selection of investments and their share in the portfolio represents the ideal investment strategy based on the data trends.
The Science Behind the Modern Portfolio Theory
Let’s understand the mathematics behind MPT. However, first, we must understand a few key terms that make the mathematical model possible.
- Expected Return: This is the percentage return expected from an investment. It can be calculated using statistical analysis of historical trends.
- Standard Deviation: This quantifies the volatility of a particular financial asset. It is the measure of risk associated with an investment, i.e., a high variance asset carries high risk and high reward. It is also estimated using statistical analysis of the data trends.
- Covariance: This estimates the relationship between the different assets. Covariance helps optimize the portfolio distribution by changing the asset weights depending on the covariances.
Given three stocks, A, B, and C, let’s build a portfolio. An investor aims to figure out how many funds to allocate to either stock. For the given stocks, let's assume each stock holds the following features.
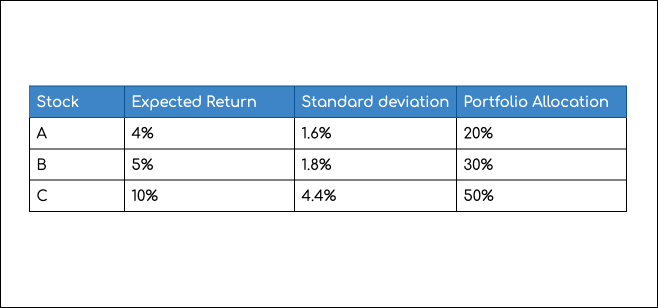
If the total investment amount is $1000, $200 is for Stock A, $300 for B, and $500 for C. Given the distribution, the mean portfolio return comes out to be.

The allocation percentages are also considered the profile’s weights as they determine how much investment goes into which asset.
The second important factor to consider here is the portfolio's variance or Risk. Portfolio risk is trickier to calculate as it considers the covariance of the different assets. An optimal portfolio under the Markowitz model includes assets with a negative correlation. If a particular asset declines, another will rise and counter its loss, reducing the overall portfolio's risk.
The formula for a portfolio variance becomes

The covariance needs to be calculated for each asset pair in the portfolio. Let’s assume our assets have the following correlation matrix.

Considering the correlation values and the above standard deviation, we can calculate the covariances using the following formula:

The covariance matrix becomes

Using the above-calculated values, our portfolio co-variance becomes

Efficient Frontier
The above example displays one possibility for an investment portfolio. Markowitz’s theory creates multiple combinations of such portfolios using different allocation (weights) values. The different portfolios display various levels of returns for a given risk value (variance). These different portfolios are visualized on a chart called the Efficient Frontier.
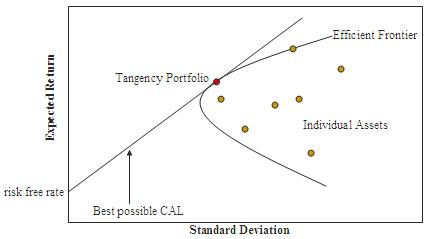
The curve represents a risk-reward trade-off where investors are interested in everything above the line. Another interesting factor of this chart is the Capital Allocation line (CAL) that runs from the risk-free point (Zero Standard-Deviation) and forms a tangent across the curve. The tangent point has the highest reward-to-risk ratio and is the best possible portfolio for investment.
Key Takeaways
An investment portfolio comprises various assets such as stocks and bonds. Every investor starts with a fixed investment capital and decides how much to invest in each asset. Data science techniques such as the Markowitz mean-variance theory help determine the optimal share allocation to build the optimal portfolio.
The theory formulates a mathematical model to optimize the asset allocations to gain the maximum return for a given risk-level. It analyzes different financial assets and considers their rate of return and risk factors, given their historical trends. The rate of return is an approximation of how much profit the asset will generate over a given time period. The risk factor is quantified using the standard deviation of the asset value. A higher deviation represents a volatile asset and, hence, higher risk.
The return and risk values are calculated for various portfolio combinations and are represented on the efficient frontier curve. The curve helps investors determine the highest returns against their selected risk.

