Author:
(1) Brandon T. Willard, Normal Computing;
(2) R´emi Louf, Normal Computing.
Table of Links
- Abstract and Intro
- LLM Sampling and Guided Generation
- Iterative FSM Processing and Indexing
- Extensions to Iterative Parsing
- Discussion, References and Acknowledgments
4. Extensions to Iterative Parsing
In this section, we move our focus to general parser-guided generation and start with a simple walk-through for a Python-like grammar provided as a CFG.
Consider a vocabulary consisting of strings like "d" and "ef" that can be combined to produce Python-like syntax according to an implicit CFG, and assume that these strings are sequentially sampled and concatenated according to a process like Algorithm 1.
Furthermore, consider a terminal symbol DEF in the CFG that corresponds to the string "def" and is given by the trivial regular expression def. Also, consider a NAME symbol given by the regular expression [^\W\d]\w* (e.g. Python identifiers). We want to sequentially parse strings sampled from the aforementioned vocabulary in a way that adheres the Python syntax.
For example, the following could be one such sequence: ["d", "ef", " f", "oo(", "):", " ", "pass"]. All the elements of the sequence are by definition elements of the vocabulary. Concatenating the sequence produces "def foo(): pass", which is a valid sequence of tokens defining a function. In the situation we’re considering, we will have observed all the tokens up to a certain point and know nothing about the ones after that point.
For instance, at the third observation in the example sequence, we have the concatenated string "def f". If we were to lex/parse this string a traditional approach would return the symbol sequence DEF NAME, which misidentifies the "f" as a complete NAME token. As we can see from the rest of the sequence, the correct NAME token will be "foo".
In general, the next valid strings that can be sampled from the vocabulary are ones that either
-
continue expanding/advancing the NAME currently starting with "f" (as the full sequence in our example does), and/or
-
anything that begins with "("–i.e. an LPAR symbol with regular expression (–and proceeds to specify a valid argument signature.
In the first case, the "f" can be seen as a partially matched NAME symbol in Python, and–recalling that its regular expression is [^\W\d]\w*–we can say that it matches both sub-patterns (i.e. [^\W\d] and \w*) in the regular expression. Our use of FSMs formalize the notion of sub-patterns by way of an FSM’s states. In this case, the regex for NAME can be represented by an FSM, M, with three states: 0 (i.e. the initial state q0), 1 (i.e. [^\W\d]), and 2 (i.e. \w*), where 1, 2 ∈ F.
Using Algorithm 3, we would obtain the FSM state sequences (0, 1), (1, 2), (2, 2) for "f" and the FSM, M, corresponding to the NAME symbol. These FSM sequences for "f" tell us that matching can start for this vocabulary string in the states 0, 1, or 2, and it can end in states 1 or 2.
According to case 1. above, parsing can be continued–for the NAME symbol–after previously ending in states 1 or 2. According to case 2., the next string could also start with or contain an LPAR, implying that M would have terminated, which it can given that 1 and 2 are final states in M at which the parsing would have stopped after reading "f". M terminating also indicates that a NAME symbol was completed, and that a transition to a state accepting LPAR was allowed by the grammar.
In this illustration, the next valid vocabulary strings are at least "d", "ef", "pass", " ", "oo(", because all of those strings would expand the partially matched NAME, and the last one would also progress the parse state to one that reads an LPAR. The remaining string, "):", from the subset of the vocabulary we’ve considered would result in a sequence with invalid syntax.
In relation to the FSM indexing approach, this means that Algorithm 4 would map FSM states 0, 1, and 2 to the subset "d", "ef", "pass", " ", "oo(" for the symbol NAME and its FSM, M.
This illustration omits the underlying parser states that determine which grammar symbols and transitions are allowed. We use pushdown automata (PDA) as a means to extend the FSM approach and address the remaining details.
4.1 Pushdown Automata Formulation
We define pushdown automata using the following 6-tuple representation [Sipser, 1996, Definition 2.13]:
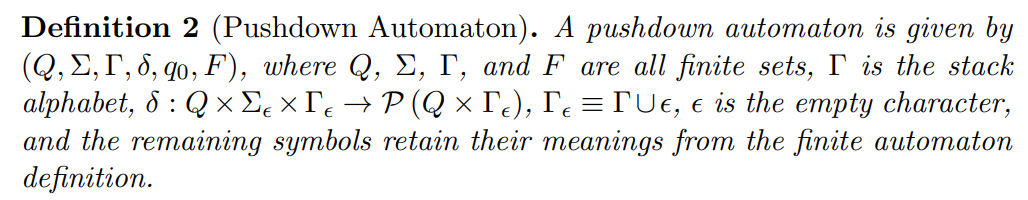
In order to construct an indexing approach for a PDA-driven parser, we need to use the connection between a CFG’s symbols–via a corresponding PDA’s alphabet–and the lexing and scanning steps that produce the symbols read by a PDA.
More specifically, parsers are supported by lexers and scanners that identify symbols from a sequence of character inputs, as we implicitly illustrated in Section 4. Ordered lists of terminal symbols can be constructed for each parse/PDA state based on the symbol and stack transitions allowed by the map δ in each state. This means that we can construct an FSM for each parse state that is the union of each FSM corresponding to a terminal symbols read by the state.
A scanning step will then identify a set of possible terminal symbols V ⊂ Σ for the characters read since the last fully identified symbol in the parsing process. For example, in the initial state q0 of a PDA for the Pythonlike CFG in Section 4, scanning and lexing the string "de" will result in V = {DEF, NAME}: i.e. DEF for any vocabulary string completing the string "def"–followed by a string not also read by the NAME FSM (e.g. "def ")– and NAME for any other strings read by its FSM (e.g. "default"). Note that steps of the scanner–and sampling steps of the LLM–will eventually reduce the set V until a single terminal symbol v ∈ V is determined.
By applying Algorithm 3 to each string in V using the combined FSMs for each parse state, we can determine parser configurations that consist of the PDA states, the corresponding FSM states, and the potential terminal symbols.
By analogy with the steps in Algorithm 3, we can use the pre-image of the PDA’s transition map to determine PDA stack values that will read the PDA states q ∈ Q and terminal symbol sets V of a parser configuration:
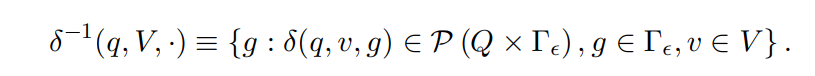
The stack values provided by this map are needed in order to find paths– if any–through the PDA that allow successful, complete parses of each string in V starting from their possible parser configurations. For parser state and terminal combinations that correspond to REDUCE operations of an LALR(1) parser, these parser configurations will consist of more than just the topof-stack values in Γ; they will consist of sub-stacks corresponding to all valid prefixes for the REDUCE operations entailed by a vocabulary string. Ultimately, each parser configuration that permits a complete parse of a vocabulary string is added as an entry in the index for the PDA, and, in this case, the index will need to be a trie data structure in order to allow queries against the parser’s stack values.
This paper is available on arxiv under CC 4.0 license.
