Imagine yourself as the proud owner of a souvenir shop inside the Spot-On Change Hotel. When closing the cash register, you notice an excess of 8 euros. It seems that a guest didn’t receive the exact change. This could tarnish the hotel’s reputation. To avoid this, you decide to solve the mystery of the incorrect change. Upon opening the shop’s cash system, you discover that the error occurred on two different accounts!
You devise a plan: to visit each room and ask the guests what change they received in the shop until you find the two with the wrong bill. Arriving on the first floor, a guest reports receiving 4 euros in change. You calculate that you need to find a number that, when added to the 4 euros, results in 8. Moving to the second floor, the guest’s change is 5 euros. 4 + 5 results in 9, so it can’t be this one… Fifth floor, sixth… Tenth, NO, NO, NO!
Since you didn’t find the value on the first attempt, you go down to the second floor and start asking all the guests again about their change so that you can compare it with the value from the next starting floor, exhausting, isn’t it? In computer science, this search method is called brute force, an extremely slow search method that works by comparing one item with the following ones in the array.
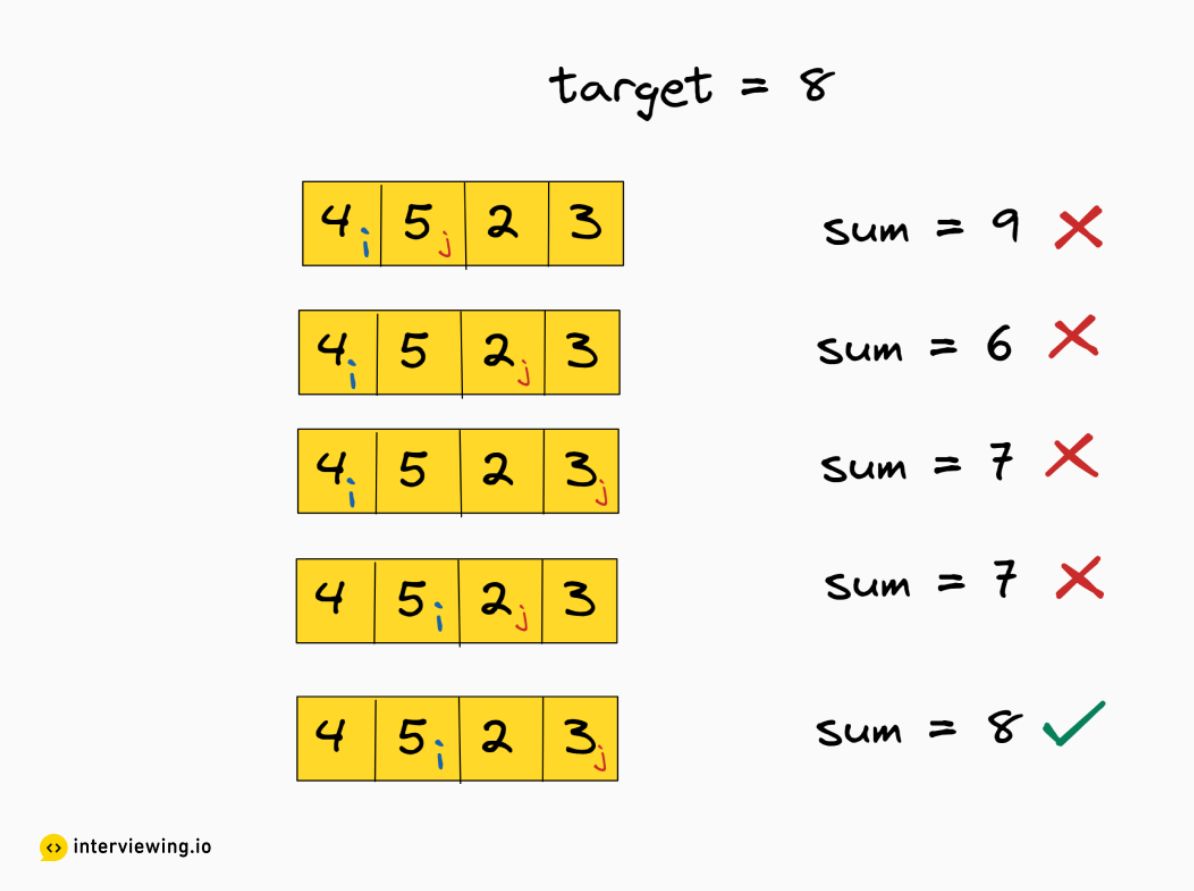
This consumes a lot of time and is not efficient, imagine going up and down all the floors of the Spot-On Change Hotel several times! This is not practical for you and also not practical for the computer.
If you’re curious about how this going up and down the floors would be in a software program, it would look like this in JavaScript:
twoSum(nums, target) {
for (let i = 0; i < nums.length; i++) {
for (let j = i + 1; j < nums.length; j++) {
if (nums[i] + nums[j] === target) {
return [i, j];
}
}
}
}
After assessing the situation calmly, you realize that there’s a more efficient way to find the two guests with the wrong change.
You refine your initial mathematical intuition that 9 euros equals x + y. Applying a bit of arithmetic, you realize that: x + y = 9 is the same as saying that y = 9 — x, and that makes all the difference when increasing the efficiency of your search.
Another thing that changed in your strategy is that now you will take a notepad to write down the values that the guests tell you, so you don’t have to ask the same value twice for the guests, and you don’t have to spend the day going up and down stairs. (What a terrible time for the elevator to break!).
With the new tools in hand, you head to the first floor, where a guest informs you that they have 5 euros in change. You record this as {5: 0}, indicating a value of 5 at position 0. Substituting x with 5 in the equation, you calculate y = 8–5, resulting in y = 3. Since your notepad is still empty, you don’t have the number 3 recorded, which would be the complementary number to 5 to reach the result 8. You then write down the number 5 on your notepad (remember to always write down the number verified at the moment and not its complement; you will only use the complement to compare it with the target number that you have written down). You proceed to the second guest, who mentions receiving 2 euros in change. Applying the formula again: y = 8–2 => y = 6, you check your record, where you don’t find any number 6. Thus, you add the 2 to your record, which now stands as {5: 0, 2: 1}. Continuing the search, the next guest reports receiving 3 euros in change. You calculate again: y = 8–3 => y = 5. Bingo! You have a 5 recorded on your notepad! The guest from floor 0 is complementary to the one from floor 2! This approach is known as a hash table, and it’s much faster and efficient, both for you and the computer. In JavaScript, this would be implemented as follows:
twoSum(nums, target) {
const myTable = {};
for (let i = 0; i < nums.length; i++) {
const complementaryNumber = target - nums[i];
if (complementaryNumber in myTable) {
return [i, myTable[complementaryNumber]];
}
myTable[nums[i]] = i;
}
}
This is an easy problem from Leetcode that only becomes easy after you understand the concepts behind it. I recommend that you try to solve the problem on your own and spend some time trying to build intuition behind it, create your own analogy, review, and try to write pseudocode before moving on to the solution.
I hope my analogy has helped you better understand the concepts behind the two sum challenge.
See you next time!
