Authors:
(1) Praneet Prakash, Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom (Email: pp467@cam.ac.uk);
(2) Yasa Baig, Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom (Email: ymb27@cam.ac.uk);
(3) Francois J. Peaudecerf, Institute de Physique de Rennes, Universite Rennes, UMR 6251, F-35000 Rennes, France (Email: francois.peaudecerf@univ-rennes1.fr);
(4) Raymond E. Goldstein, Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom (Email: R.E.Goldstein@damtp.cam.ac.uk).
Table of Links
Anti-Diffusion in an Algae-Bacteria Microcosm: Photosynthesis, Chemotaxis, and Expulsion
In Nature there are significant relationships known between microorganisms from two kingdoms of life, as in the supply of vitamin B12 by bacteria to algae. Such interactions motivate general investigations into the spatio-temporal dynamics of metabolite exchanges. Here we study by experiment and theory a model system: a coculture of the bacterium B. subtilis, an obligate aerobe that is chemotactic to oxygen, and a nonmotile mutant of the alga C. reinhardtii, which photosynthetically produces oxygen when illuminated. Strikingly, when a shaft of light illuminates a thin, initially uniform suspension of the two, the chemotactic influx of bacteria to the photosynthetically active region leads to expulsion of the algae from that area. This effect arises from algal transport due to spatially-varying collective behavior of bacteria, and is mathematically related to the “turbulent diamagnetism” associated with magnetic flux expulsion in stars.
In the early 1880s the biologist Theodor Engelmann performed experiments that were perhaps the first to use bacteria as sensors [1–3]. Several years prior he made the first observation of bacterial chemotaxis toward oxygen, by showing that putrefactive bacteria would migrate toward the chloroplasts of the filamentous alga Spirogyra. He then determined the “action spectrum” of photosynthesis—the wavelength-dependent rate of photosynthetic activity—by passing sunlight through a prism and projecting the spectrum onto a filamentous green algae held in a chamber that contained those self-same bacteria, which gathered around the algae in proportion to the local oxygen concentration, providing a direct readout of the oxygen production rate.
Although Engelmann’s system was engineered for a particular purpose, and at first glance involves a oneway exchange of oxygen for the benefit of bacteria, there are many examples of mutualistic exchanges between microorganisms from two distinct kingdoms of life. One of the most significant is that involving vitamin B12. In a landmark study [4], it was shown that a significant fraction of green algae that require this vitamin for their metabolism do not produce it, and as the ambient concentration of B12 in the aqueous environment is so low, they instead acquire it from a mutualistic relationship with bacteria, which benefit from a source of carbon.
The study of B12 transfer raises fascinating questions in biological physics related to the interplay of metabolite production, chemotaxis, and growth [5], including the issue of how organisms find each other and stay together in the turbulent environment of the ocean, and how advection by fluid flows arising from microorganism motility affects such mutualisms. As it is difficult to control the production of vitamin B12, we sought to construct a system in which the production of a chemical species needed by one member of an interacting pair of organisms could be controlled by the experimentalist. Taking motivation both from Engelmann’s experiments and the B12 system, we introduce here a coculture [6] in which an obligate aerobic bacterium (one that requires oxygen) that is chemotactic toward oxygen, coexists with a green alga whose photosynthetic activity can be turned on and off simply by controlling the external illumination.
We use the bacterium Bacillus subtilis, whose aerotaxis has been central in the study of bioconvection [7] and in the discovery of “bacterial turbulence” [8], the dynamical state of a concentrated suspension with transient, recurring vortices and jets of collective swimming on scales large compared to the individual bacteria. The alga species is the well-studied unicellular Chlamydomonas reinhardtii, a model organism for biological fluid dynamics [9] with readily available motility mutants useful in probing the role of swimming in metabolite transfer. Together these define what we term the algae-bacteriachemoattractant system (ABC). While coupled population dynamics problems have been studied from the familiar reaction-diffusion point of view in bacterial range expansion [10], marine [11] and more general ecological contexts [12], we show that there are physical effects that go beyond that standard level of treatment. Chief among them is the way in which collective motion can act as a “thermal bath” in enhancing the diffusivity of suspended particles [13, 14], which in turn raises fundamental issues concerning generalizations of Fick’s law [15, 16].
A disarmingly simple experiment to understand the dynamics of the ABC system involves a thin, quasi-twodimensional suspension of non-motile algae and fluorescently labelled bacteria at initially uniform concentrations. As depicted in Fig. 1, a shaft of photosynthetically active light is cast on the suspension, triggering oxygen production by the illuminated algae. As shown in Figs. 2(a,b), this leads to chemotaxis of bacteria into the illuminated region, producing a high concentration of bacteria. Remarkably, we find that algae are then expelled
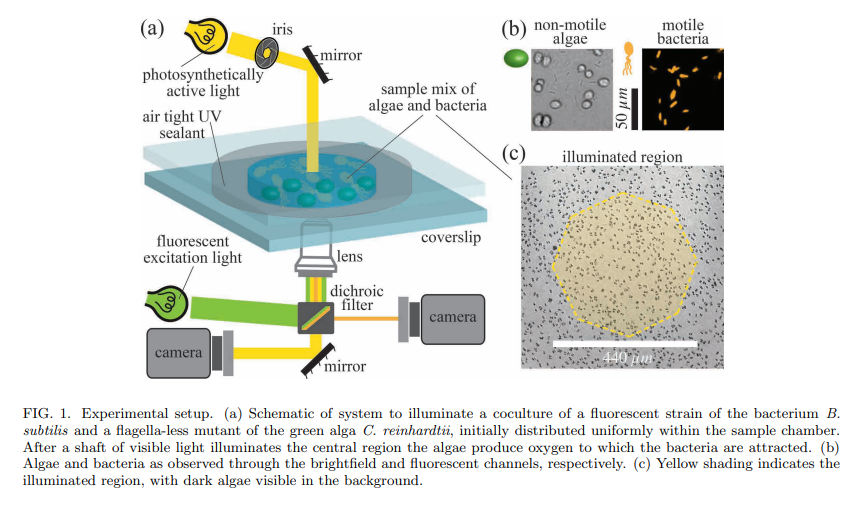
from the illuminated region. Quantitative measurements of the local bacterial dynamics in the the system show that this expulsion is associated with a gradient of collective bacterial behavior from its peak at the center, leading to a outward algal transport. On longer time scales, after the algal expulsion, the bacterial concentration returns to uniformity as the bacteria diffusive outward in the absence of chemotactic stimulus. We name this Type I dynamics. Figures 2(c,d) show that at sufficiently high initial bacterial concentrations a new, Type II behavior is observed; expulsion of alga and consumption of oxygen are sufficiently rapid that many bacteria in the illuminated region become hypoxic, transition to an immotile state, and are then also expelled into the dark.
We develop here a system of coupled PDEs that describes the ABC system that provides a quantitative account of the experimental observations. These PDEs incorporate diffusion, chemotaxis, oxygen production and consumption and algal transport by collective effects. The expulsion of algae is similar to well-known processes in magnetohydrodynamics termed “flux expulsion”. First discovered for magnetic fields in a prescribed constant vortical flow field [17], in which field lines are expelled from the vortex, it was later recognized that this expulsion can arise from gradients in the intensity of turbulence whose random advection of the magnetic vector potential leads to a gradient in its effective diffusivity and thence to “turbulent diamagnetism” [18].
Methods.— The coculture used strain 168 of B. subtilis which was genetically engineered to express yellow fluorescent protein m-Venus with excitation at 515 nm and emission at 528 nm [19]. A single bacterial colony was picked from an agar plate and grown overnight in Terrific Broth (TB) on an orbital shaker at 240 rpm and 30 ◦C. The bacteria intended for experiments were grown from overnight culture until exponential growth phase in Tris-min medium spiked with TB medium (Tris-min + 0.1 % w/v glycerol + 5 % w/v TB). The non-motile C. reinhardtii strain CC477 (bld1-1) was sourced from the Chlamydomonas Resource Center [20] and grown in Trismin medium, on an orbital shaker at 240 rpm and 20 ◦C. The diurnal cycle was 12 h cool white light (∼ 15 µmol photons/m2 s PAR), and 12 h in the dark.


Experiments were performed on a Nikon TE2000-U inverted microscope. The spatio-temporal variation in bacterial concentration was monitored by epifluorescence illumination with a ×20 objective using a highly sensitive, back-illuminated camera (Teledyne Prime Σ 95B). Movies of algae cells were recorded through the brightfield channel using a Phantom V311 high-speed camera (Vision Research) at ×20 magnification. The halogen lamp served as both a brightfield and photosynthetic light source. The size of a light shaft used to trigger photosynthesis was controlled by the field iris in the microscope condenser arm, producing an octogonal boundary in the focal plane with mean radius of R = 220 µm.

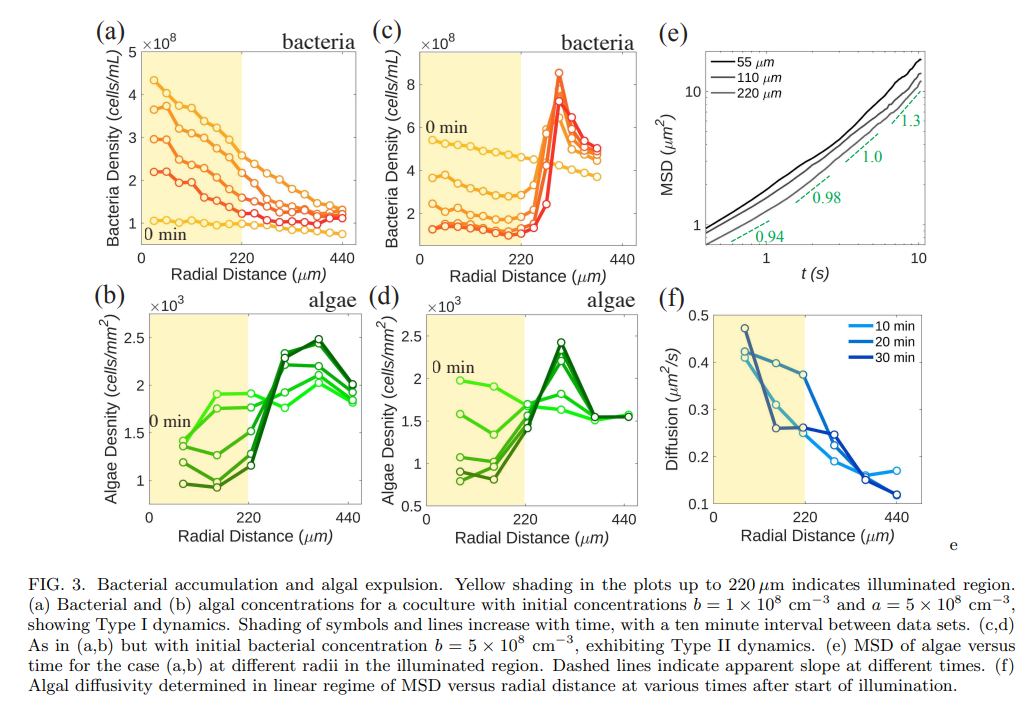





Figures 4(a,b) show how the model defined by Eqs. (3), (5) and (7b) provide a quantitative fit to the observed Type I dynamics. In particular, we see the prompt accumulation of bacteria in the illuminated region followed by expulsion of algae. In the model and in experiment, the fraction of algae ultimately expelled is ∼ 0.5, so there is still oxygen production within the illuminated region after ∼ 30 min, leading to continued chemotactic attraction of bacteria inward. This leads to a slower decay of the bacterial concentration back to its original uniform, low value than seen in experiment. This may reflect processes such as bacterial adaptation to the oxygen and a gradual reduction in oxygen production by algae.
The ABCD model.— While the ABC model can account for the essential features of Type I dynamics, it does not allow for loss of motility of bacteria at low oxygen concentrations in Type II dynamics. This transformation has been recognized as important in the context of bioconvection [21, 23], where the influx of oxygen at the air-water interface of a bacterial suspension competes with consumption within the fluid, leading to a hypoxic region hundreds of microns below the surface. Hypoxiainduced motility transitions have also been observed in the penetration of oxygen into suspensions of E. coli [24]. To account for this transformation we view the “dormant”, non-motile state of the bacteria, with concentration d, as a separate population distinct from the motile form, so the extended “ABCD” model involves algae, bacteria, chemoattractant, and dormant bacteria. The interconversion rate as a function of oxygen concentration c is taken as a simple generalization of the substrate-dependent growth of the Monod model, vconbKsat/(c + Ksat), where vcon is the maximum conversion rate to the immotile form and Ksat is the concentration at which half-maximal conversion occurs.

Spatially-averaged model.— Insight into the basic process of algal expulsion can be obtained by constructing a spatially-averaged model which takes as dynamical degrees of freedom the mean concentrations of algae, bacteria, and oxygen inside the illuminated region, denoted by ¯α, β¯, and ¯χ. As indicated schematically in Fig. 5(a), the specification of this averaged model requires estimates of the various fluxes across the boundary of the
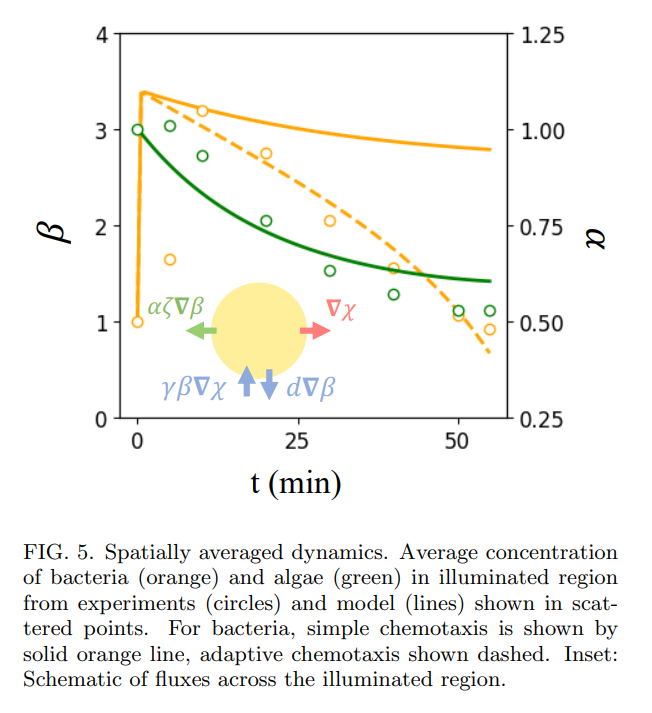

Similar estimates hold for the averaged bacteria dynamics, where the relevant fluxes are the outward diffusive and inward chemotactic contributions. The diffusive contribution is precisely analogous to that for oxygen above. Since on the time scales of the experiment only bacteria within a distance λ outside the illuminated region sense the gradient, the inward Keller-Segel flux is also estimated as above, but with an upper limit on the bacterial concentration due to steric effects. This leads to the ODE version of (5),

Discussion.— As our results suggest new phenomenology in active matter systems, it is instructive to return to the connection between algal expulsion and flux expulsion in magnetohydrodynamics. In the original case considered [17], a magnetic field in a fluid with velocity u obeys the Maxwell equation,

This form has the same structure as our Eq. (7a), with the bacterial concentration β playing the role of the diffusivity tensor component. We conclude that the main difference between the two problems is the expulsion of a scalar (concentration) field in the present context compared to the expulsion of a vector quantity in MHD.
The results described here highlight the rich dynamical behavior that occurs in mixed active matter systems involving microorganisms from two Kingdoms of Life. While the dynamics of symbiosis is generally studied on time scales relevant to population dynamics or evolution [25–27], our findings indicate that short-term dynamics on the scale of minutes and hours can have a considerable impact on the spatial-temporal aspects of association, where chemotaxis and phenotypic switching dominate. Although we considered the simple case of light intensity that is piecewise constant, inhomogeneous activity arises. The treatment of such nonuniform active matter has received attention only recently, in the context of “invasion” [28] and active gels [29], but is central to any discussion of realistic ecologies. In this sense, generalizing the present setup to allow algal motility and phototaxis in the presence of an inhomogeneous light field may reveal even more striking dynamics when the oxygen sources are themselves motile.
We are grateful to Jim Haseloff for providing the fluorescent strain of B. subtilis and to Kyriacos Leptos for numerous discussions. This work was supported in part by the Gordon and Betty Moore Foundation, Grant No. 7523 (PP & REG) and the U.K. Marshall Aid Commemoration Commission (YB).
[1] T.W. Engelmann, Ueber Sauerstoffausscheidung von Pflanzenzellen im Microspectrum, Archiv f¨ur die gesamte Physiologie des Menschen und der Tiere 27, 485-489 (1882).
[2] G. Drews, Contributions of Theodor Wilhelm Engelman on phototaxis, chemotaxis, and photosynthesis, Photosynth. Res. 83, 25–34 (2005).
[3] R.E. Goldstein, Coffee stains, cell receptors, and time crystals: Lessons from the old literature, Phys. Today 71, 32–38 (2018).
[4] M.T. Croft, A.D. Lawrence, E. Raux-Deery, M.J. Warren, and A.G. Smith, Algae acquire vitamin B12 through a symbiotic relationship with bacteria, Nature 438, 90– 93 (2005).
[5] F.J. Peaudecerf, F. Bunbury, V. Bhardwaj, M.A. Bees, A.G. Smith, R.E. Goldstein, and O. Croze, Mutualism Between Microbial Populations in Structured Environments: The Role of Geometry in Diffusive Exchanges, Phys. Rev. E 97, 022411 (2018).
[6] F.J. Peaudecerf, Ph.D. thesis, Mathematics, University of Cambridge (2017).
[7] T.J. Pedley and J.O. Kessler, Hydrodynamic phenomena in suspensions of swimming microorganisms, Annu. Rev. Fluid Mech. 24, 313-358 (1992).
[8] C. Dombrowski, L. Cisneros, S. Chatkaew, J.O. Kessler, and R.E. Goldstein, Self-concentration and large-scale coherence in bacterial dynamics, Phys. Rev. Lett. 93, 098103 (2004).
[9] R.E. Goldstein, Green algae as model organisms for biological fluid dynamics, Annu. Rev. Fluid Dynamics 47, 343–375 (2015).
[10] J. Cremer, T. Honda, Y. Tang, J. Wong-Ng, M. Vergassola, and T. Hwa, Chemotaxis as a navigation strategy to boost range expansion, Nature 575, 658–663 (2019).
[11] H. Malchow, Spatio-temporal pattern formation in nonlinear non-equilibrium plankton dynamics, Proc. R. Soc. B 251, 103–109 (1993).
[12] R. Martinez-Garcia, C.E. Tarnita, and J.A. Bonachela, Spatial patterns in ecological systems: from microbial colonies to landscapes, Emerg. Top. Life Sciences 6, 245– 258 (2022).
[13] X.-L. Wu and A. Libchaber, Particle Diffusion in a QuasiTwo-Dimensional Bacterial Bath, Phys. Rev. Lett. 84, 3017–3020 (2000).
[14] K.C. Leptos, J.S. Guasto, J.P. Gollub, A.I. Pesci, and R.E. Goldstein, Dynamics of enhanced trancer diffusion in suspensions of swimming eukaryotic microorganisms, Phys. Rev. Lett. 103, 198103 (2009).
[15] M.J. Schnitzer, Theory of continuum random walks and application to chemotaxis, Phys. Rev. E 48, 2553–2568 (1993).
[16] A.W.C. Lau and T.C. Lubensky, State-dependent diffusion: Thermodynamic consistency and its path integral formulation, Phys. Rev. E 76, 011123 (2007).
[17] N.O. Weiss, The Expulsion of Magnetic Flux by Eddies, Proc. R. Soc. A 293, 310–328 (1966).
[18] L. Tao, M.R.E. Proctor, and N.O. Weiss, Flux expulsion by inhomogeneous turbulence, Mon. Not. R. Astron. Soc. 300, 907–914 (1998).
[19] P.J. Steiner, Ph.D. thesis, Plant Science, University of Cambridge (2017).
[20] https://www.chlamycollection.org/
[21] I. Tuval, L. Cisneros, C. Dombrowski, C.W. Wolgemuth, J.O. Kessler, and R.E. Goldstein, Bacterial swimming and oxygen transport near contact lines, Proc. Natl. Acad. Sci. USA 102, 2277-2282 (2005).
[22] E.F. Keller and L.A. Segel, Model for chemotaxis, J. Theor. Biol. 30, 225-234 (1971).
[23] A.J. Hillesdon, T.J. Pedley, and J.O. Kessler, The development of concentration gradients in a suspension of chemotactic bacteria, Bull. Math. Biol. 57, 299-344 (1995).
[24] C. Douarche, A. Buguin, H. Salman, and A. Libchaber, E. coli and oxygen: A motility transition, Phys. Rev. Lett. 102, 198101 (2009).
[25] V. Piskovsky, N. Oliveira, Bacterial motility can govern the dynamics of antibiotic resistance evolution, Nature Communications 14, (2023).
[26] Y. Baig, H.R. Ma, H. Xu, L. You, Autoencoder neural networks enable low dimensional structure analyses of microbial growth dynamics, Nat Commun. 14(1), 7937 (2023).
[27] L. David, C. Maurice, R. Carmody, D. Gootenberg, J. Button, B. Wolfe, A. Ling, A. Devlin, Y. Varma, M. Fischbach, S. Biddinger, R. Dutton, P. Turnbaugh, Diet rapidly and reproducibly alters the gut microbiome, Nature 505, (2013).
[28] C.J. Miles, A.A. Evans, M.J. Shelley, and S.E. Spagnolie, Active matter invasion of a viscous fluid: Unstable sheets and a no-flow theorem, Phys. Rev. Lett. 122, 098002 (2019).
[29] R. Assante, D. Corbett, D. Marenduzzo, and A. Morozov, Active turbulence and spontaneous phase separation in inhomogeneous extensile active gels, Soft Matter 19, 189–198 (2023).
This paper is available on arxiv under CC 4.0 license.

