Reason is what we learn from the world, and creativity is what we bring to it. In this sense, each scientific journey is a glimpse into both our universe and the one we live in. The quantum universe outside is one of the most intriguing and exciting fields of science. But as with any field of science, it does not come with its own impartial knowledge or seeming paradoxical nature. In this exploration, we are going to dive into the very heart of atoms, sit on the nucleus that shapes them, and watch the electrons above spin around us at mind-dazzling speeds.
Introduction
Atoms are the most basic and fundamental building blocks that shape our reality. They are composed of protons, neutrons, and electrons. The components of an atom are called particles, and they play a role in shaping the overall atom.
- A proton is a positively charged subatomic particle found in the nucleus of an atom. It has a mass of 1 atomic mass unit (amu) and carries a charge of +1 elementary charge. The number of protons is equal to the number of electrons. This number is called an atomic number.
- A neutron is a neutral subatomic particle found also in the nucleus. It has a mass of 1 amu, and unlike protons, it carries no electrical charge. Neutrons have the role of holding the nucleus together by counteracting the repulsive electromagnetic force of protons. Their number can vary. This variation is responsible for different isotopes of the same element. For example, the most common isotope of carbon is carbon-12, which holds 6 protons and 6 neutrons. Other isotopes are: carbon-13 (6 protons, 7 neutrons); carbon-14 (6 protons, 8 neutrons). Some isotopes are stable; others are less stable and will eventually decay into other elements.
- An electron is a negatively charged subatomic particle that orbits the nucleus. It has a mass of approximately 1/1836 amu and carries a charge of -1 elementary charge. Electrons play a crucial role in atomic bonding as they can be shared between the different nuclei of the bonded atoms. The behavior of electrons within atoms is described by quantum mechanics, which explains the various energy levels and orbitals they occupy.
To aid in visualization, I will provide some images (forgive my editing skills).
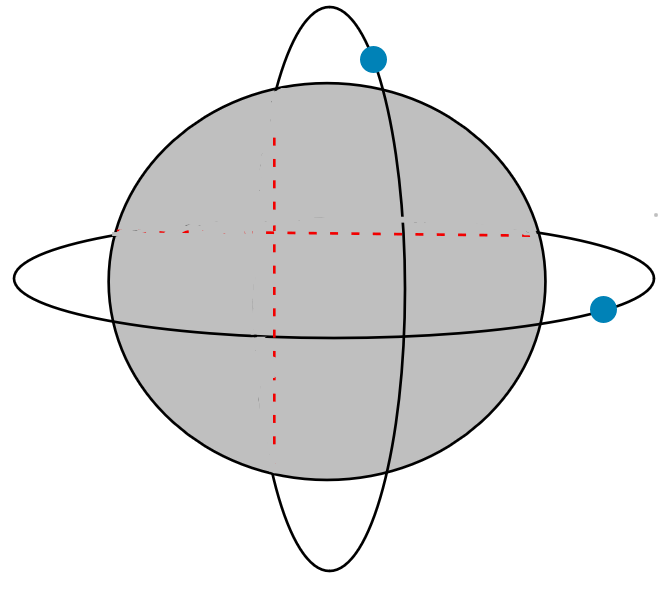
The big gray circle represents the nucleus, which is made up of the respective numbers of protons and neutrons. The circles around it are the respective spinning paths of each blue electron. The red dotted line is the unseen path.
Of course, in reality, the nucleus is made up of multiple tiny particles and is not quite a circle, and the electrons spin at much longer relative distances than the ones drawn. Richard Feynman said, “If you think you understand quantum mechanics, you then don't.” Reflecting the inherent undepictable nature of multiple atoms and their interactions over time, as well as the extremely complex task of showcasing the precise behavior of the electrons in the system. Heisenberg’s uncertainty principle also states that we cannot know both the momentum (speed) and the location of an electron at the same time. The tools used to analyze and understand quantum mechanics are mind-bending to understand. I mean, Schrodinger’s equation looks like this: iℏ ∂/∂t |Ψ(t)⟩ = Ĥ |Ψ(t)⟩. And the role of the equation is to determine the evolution of a quantum system over time. Or, more precisely, single- and multiple-atom systems behavior.
So that’s a lot to wrap our heads around. However, the only thing we will require further from this equation is i, the imaginary unit.
Part 1: Imaginary
Numbers are great. They can be positive (+1), negative (-1), or neutral (0). We can add, subtract, multiply, divide, raise them to a power, or find their logarithmic value. Adding a number to itself multiple times means multiplying it. Multiplying a number by itself multiple times means raising it to a power. 3+3+3=3×3=3^2, which is pretty cool. -3+(-3)+(-3)=(-3)×3=…-9? 3 at the power of -2 is 1 divided by 3^2, which is clearly not -9. It seems like negative numbers follow quite different rules than positive ones. That’s where i comes into play.
i is an “imaginary” number that, when raised to the power of 2, equals -1. No other number, positive or negative, has this property. As we very well know, (-)×(-)=(+) and (+)×(+)=(+). Three (-) result in (-) again, and three (+) are still (+). So, the more we multiply on the minus side, the longer the oscillation of (+)(-)(+)(-) is. The more we multiply on the plus side, the longer the static (+) is. But how about i? As stated, i×i=-1, which is negative. i itself is positive. So we have i (+), -1 (-).
Continuing to multiply i by itself further holds: -1×i, which is… -i. And another multiplication brings us to -i×i, which is -(i^2) so -(-1) and thus +1. This way, we got the loop (+)(-)(-)(+). It seems like i hold some special properties. Not only in the realm of multiplication properties but also in the realm of sign properties. If we are to draw a graph, it will look like this:
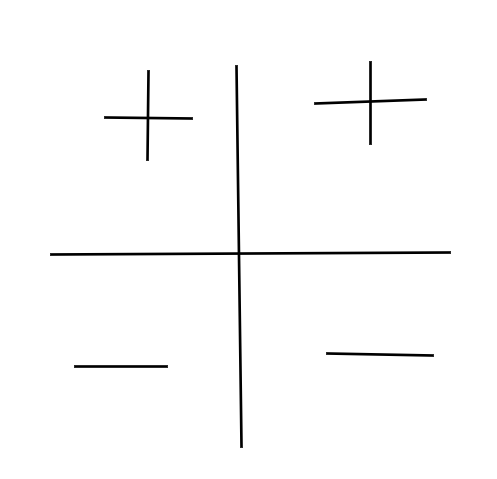
It looks like we extended the ordinary multiplication sign from 1d (either positive or negative) to 2d (left/right positive or left/right negative). So despite being called immaginary, i hold pretty real properties. Also, rigorous mathematical models and theories establish i as a real component of mathematics, and numerous physics formulas (like the Schrodinger’s equation presented) use i as a means to allow them to work.
One question you might ask yourself is: "Okay, but then, could we extend this to 3D? How would we do that?” and the answer is yes!! We could use quaternions. “Quaterni-what?"—that’s just my mind asking me where I dragged it x.x
Quaternions are considered 4-dimensional objects used to model rotation in 3d spaces. Imagine a plane that sits in the end. Rotating it head-down from a line much like the ones drawn in the atom representation. Rotating it head-left forms the other line, which is representative of the other electron. I am not going to dwell on the mathematics of quaternions yet; I can provide a second visualization. One that will allow us to understand how they might work when it comes to signs.
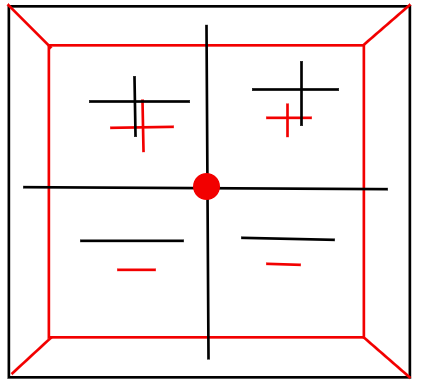
In the above image, we have a cube. This cube is split into the front side (black square) and the backside (red square). We have split it into four smaller cubes using the two black lines that split the cube into its respective areas, and the red dot at the center represents the depth line. The black pluses and minuses are those that sit on the four smaller cubes that are close to us, and the red ones reside beyond them. This is the space on which quaternions—those 4-dimensional “imaginary” objects—operate. Regarding the visual, I recommend doing your own research, as this is just my take.
Nevertheless, quaternions are extremely complex mathematical tools that could allow us, in theory, to map out the path of each and every electron within an atom. What stops us from doing it, then?
Part 2: Logic
Feynman’s words are not meant to discourage exploration or observation by simply stating that we will never find the truth about the elusive electrons. On the contrary, they speak to the truly fascinating aspects that make quantum mechanics such an intriguing field. In reality, each electron, even if it is the only electron within the atom, can circle around at multiple distances.
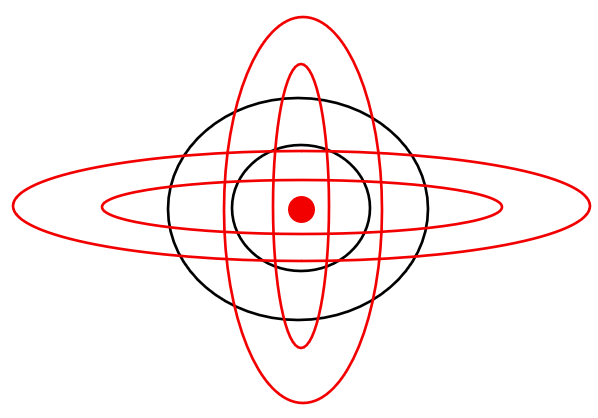
In the above image, the central dot represents the nucleus. The black circles represent two possible perfect upper-view spins, and the red ones are the side views of those two spins’ side views. After all, the electron moves in a 3D space rather than a 2D one. Now, I am not entirely sure that this is the case. Maybe electrons indeed shift their spinning area from one circle to a bigger one as they wish or as they are observed. Maybe this shift occurs with the premise that an element with multiple protons and neutrons exhibits a much greater gravitational potential, and this way, the spin area either expands or shrinks. I would vote for shrinking, as it makes sense. But then again, it’s the quantum world, so we do not know until we see.
Another possibility ties to superposition. This very interesting aspect of electrons states that, until observed, electrons are found in multiple places at the same time. Not in the way that they are situated at 75 and 180 degrees on the same circle, but rather that they are situated on two different circles at the same time. If this is to be the case, we may be able to add sine or cosine wave fluctuations in an attempt to find an anchor to grasp. And now that I mention waves let’s discuss the wave-particle duality that electrons exhibit.
The wave-particle duality is a fundamental aspect of quantum mechanics. The double-slit experiment demonstrates that if you are to shoot electrons from a central point forward and place in front of them a wall with 2 entrances situated left and right of the central part of the wall where you are shooting, the result will consist of results that resemble shooting waves. (You can search for the experiment in order to form an idea.) 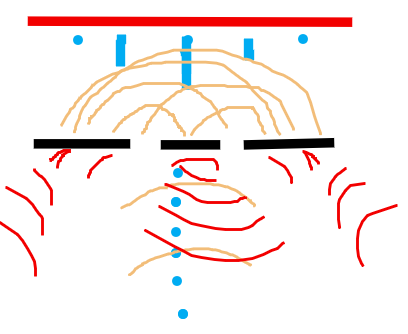 In the above image, the black wall is sectioned in the drawn way, and the red wall behind represents the area that captures the blue electrons as well as their respective numbers. The yellow lines represent my interpretation of shot "waves,” and the red lines are the part of the waves that did not make it into the gaps and are, thus, sent back. (The left and right waves might be, in reality, reflected in opposite forms.)
In the above image, the black wall is sectioned in the drawn way, and the red wall behind represents the area that captures the blue electrons as well as their respective numbers. The yellow lines represent my interpretation of shot "waves,” and the red lines are the part of the waves that did not make it into the gaps and are, thus, sent back. (The left and right waves might be, in reality, reflected in opposite forms.)
I’ve got nothing left to say. So, let’s move on to the next part, where we are going to try and find ways to collect the data found by observing an enclosed atom within a double-box area.
Part 3: Reason
Let’s reset down to factory settings and depict the atoms as such: A single electron that spins around a central nucleus. And let’s also keep in mind Heisenberg’s uncertainty principle: we cannot know both the location and the speed of an electron.
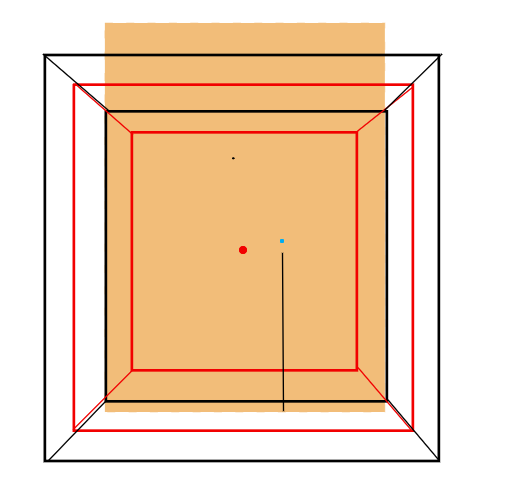
The above image tries to represent two boxes, one bigger and one smaller, inside it. The bigger box is the source of light for the smaller one. The small box has lines that allow the light to enter from above, back, and left side. On the opposite sides lie sensors that are switched to “0” when light is received and “1” when light is absent. The red dot represents the nucleus, while the blue one represents the electron. The black line that stands under the electron is the side where the electron doesn’t allow light to pass. This way, we could create a representation within the smaller box, much like the one used to describe the splitting into 4 smaller boxes used to explain how quaternions might gain their respective sign.
Now, in order to gather real-time data about the electron, we would require a room filled with light. Yet, a room filled with light will not allow for information about the location of the electron to be transmitted further. And if the light source is somehow to be the very nucleus, the spreading of light from within to outside would go in a straight manner, and thus, there would be areas in which the electron would still be unaffected by the light. This could be the very peak of limitation when it comes to depicting the exact position of an electron. But, of course, why would we need that?
One possible use case for such information could be in harnessing the power of electrons and entanglement. If entangled two atoms (i.e., they have the same starting conditions, the same properties, and the same directions of spin, thus, being exactly the same), we may be able to shoot such a box out into space, where it will tie to an object such an asteroid. We could see this quantum-sensor box as a quantum chip, which will simply store information about the location of the electron (or when it touches one of 3 2D light areas).
This information could be later transmitted using radio waves or what classical computers use to send information over a distance, and later, using sophisticated mathematics, of which I am not even sure if they exist, we could leverage the difference in spin between those two entangled particles. But of course, all that is under the assumption that electrons move close to the speed of light and that the speed of light is the ultimate limit of speed. Our Earth electron will be influenced by the movement of Earth through space, while the other will be influenced by the movement of the asteroid. In order to gather precise information, we would also require knowledge of the radio waves transmitted and the time it took them to reach us.
We see now that the gaps are ever tighter and that the sophistication required grows so exponentially that it sits at the border between possible and impossible. The mathematics we now have might simply be 5% or less of what is required. But still, the question of whether we could create a real-time holographic map of the universe makes it interesting to consider in the end. Another interesting outcome is the fact that the more we explore ideas such as Heisenberg's uncertainty principle, which might at first sound like they are limiting us, turns out, in the end, to be what allows for exploration to continue indefinitely.
Part 4: Mind-Boggling
Considering that trying to explore complexity is complex, we feel the need to reduce it to simpler terms. In our everyday lives and experiences, those terms resume to lines, circles, squares, “Hi!”, ”Thank you!”, ”Welcome!”. In the world of quantum, they, too, contain lines, circles, and squares as well as the physical and not just the mathematical and theoretic aspects of them. And why do we use that physical mathematics? To gather information about real phenomena. So even if particles welcome us into their world, their welcome is shed under the reality that even in such a double-box system, the behavior is different when the lights are on versus when they are off. And we may never know whether the mathematical models hold true until we make and play with them. But who knows how much mathematics this will require? One thing is certain, however. The end of such a story is as untouchable as the particles themselves. Light may be able to, but we cannot. Either way, both us and light influence their behavior, while mathematics guides it.
It’s a complex world out there. Out… here. While humanity is... simply beyond. It is true that our potential is endless. Our art and its depth prove it. But tying that complexity to something outside our own minds is a hard task. One that few can take. Not because the other cannot. Just as we learn from Heisenberg, our limits are not borders, but rather our very window to the world outside. There is no point in discovering an empty universe. Just as astronomers look at the skies and place their stories inside them, so too can quantum researchers place beauty in their findings. And even allow us to place our own. Who knows what avenues quantum computers could open? Well, quantum-classical ones.
I would love to continue. But time is limited, and duty calls. Good thing about parents is that they remind (and sometimes force x.x) us to see the sunlight. Even the thought of it is beautiful now. Knowing that it not only warms us but also that tiny world that sets the stage on which we step. Until we meet next time, remember to admire your limits from far, far away.
Oh, yes. Here is a picture of a bee. The next exploration could very well take into account their small world. Which, sadly, has been in increasing trouble over the past few years. But as mentioned, the potential we hold is truly endless 😄

