This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Jihoon Chung;
(2) Zhenyu (James) Kong.
Table of Links
- Abstract & Introduction
- Review of Related Work
- Proposed Research Methodology
- Numerical Case Studies
- Real-World Simulation Case Studies
- Conclusion
- References
IV. NUMERICAL CASE STUDIES
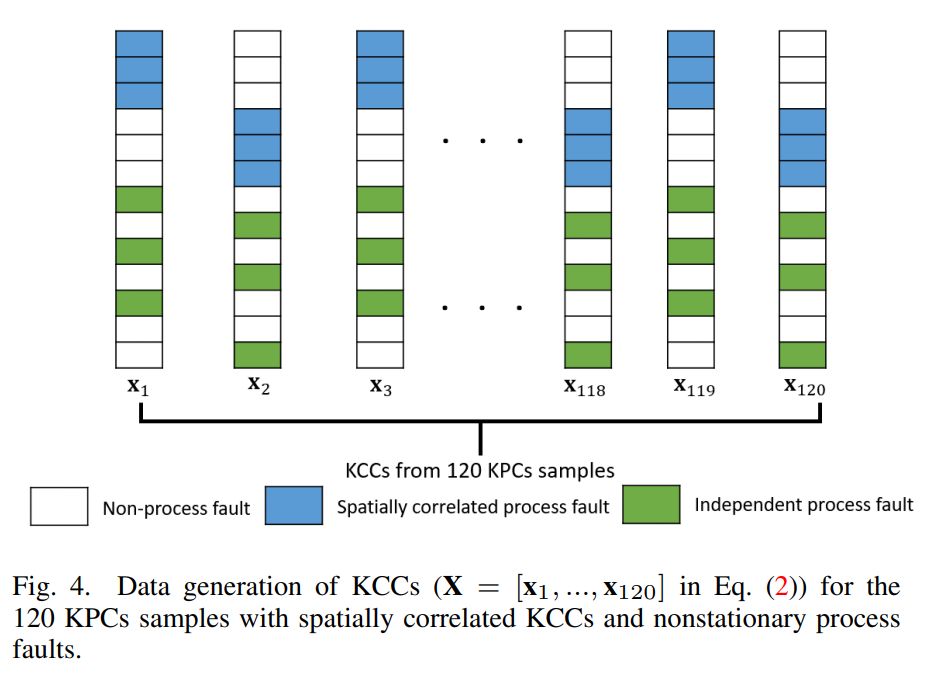
This section provides numerical studies to compare the performance between the proposed method and benchmark methods. The studies evaluate the performance by varying the correlations (ki in Eq. (7)) between the KCCs in nonstationary process faults. All the numerical case studies consist of 20 independent trials. The code of the proposed algorithm is implemented in Matlab 2021. The CPU used in case studies is an Intel® Core™ Processor i7-8750H.
This section compares the proposed method with the following benchmark methods.
• User Grouping Sparse Bayesian Learning (i.e., UGSBL) proposed in [2] is an SBL method that clusters the KPCs samples into groups sharing the same process faults in sparse estimation.
• Spatially Correlated Bayesian Learning (i.e., SCBL) proposed in [8] is an SBL method to diagnose process faults by exploiting the spatial correlation of KCCs.
• [10] proposed the SBL method that considers prior knowledge of the process faults in sparse estimation.
• MSBL proposed in [32] is a basic SBL method that assumes the independence of KCCs and stationarity of process faults.


Performance Evaluation: To evaluate the effectiveness of the proposed method, two performance measures are used in this paper. The first measure evaluates the process fault detection capability, and the second measure is related to estimation accuracy. Each measure is evaluated by varying the correlation coefficients of spatially correlated KCCs.
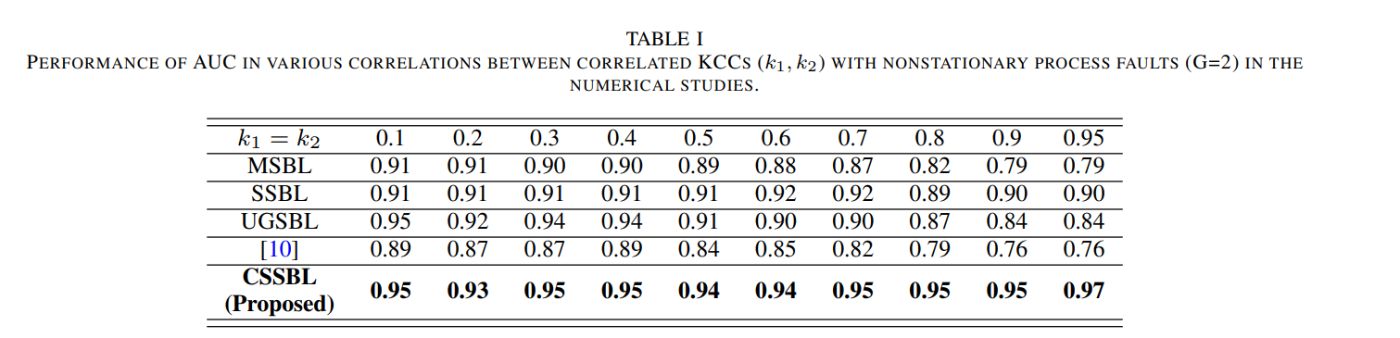
- Fault Detection Capability: First, the proposed method requires correctly identifying process faults whose KCCs have excessive variance. In order to assess the capability of detecting process faults under sparse conditions, the area under the receiver operating characteristics (ROCs) curve (AUC) is utilized [46]. AUC is widely used for evaluating the accuracy of binary classification. Specifically, AUC measures the quality of the classification accuracy between process faults and non process faults irrespective of the threshold of variance. In other words, AUC accounts for the trade-off between the type 1 and type 2 errors. When the method is capable of achieving perfect classification results, the resulting AUC value will be 1. However, the AUC with a value close to 0.5 denotes that the estimated variances of KCCs from the method are similar between the process faults and non-process faults.
Table I represents that the proposed method always achieves the best performance of AUC in the various spatial correlation between KCCs. Specifically, the AUC of the proposed method is close to 1.0 at every correlations levels, representing the perfect classification between the process faults and nonprocess faults in terms of estimated variance. Since UGSBL clusters the KPCs samples that share the same process faults, the method shows a comparable result to the proposed method when the spatial correlation of KCCs is relatively low and moderate. However, the performance degrades in the high spatial correlation since the method assumes independence between all KCCs. The performance of SSBL is robust to correlations. This is because SSBL utilizes the correlation of correlated KCCs in its estimation. However, SSBL performs worse than the proposed method since this method assumes the same process faults between all KPCs samples, which are unsuitable for dealing with nonstationary process faults. MSBL and [10] show poor performances since these methods assume the independence of KCCs and stationarity of process faults.
2) Estimation Accuracy: In addition to correctly identifying the process fault, the method needs to accurately estimate the variance of process faults. After the process faults are identified, the practitioners are interested in how large the variances are to make decisions for the maintenance of the process. To achieve this objective, this paper provides the normalized mean squared error (NMSE) between true and estimated variance.
Table II represents that the proposed method achieves the best performance in the estimation accuracy of the variance in most of the correlations. It implies that the proposed method is useful not only for the process faults identification but also for measuring how severe the process faults are. Compared to benchmark methods, the effectiveness of the proposed method in the NMSE results is noticeable in the presence of high spatial correlations between KCCs. Unlike AUC performance, the NMSE of SSBL increases as the correlation increases. It implies that SSBL successfully identifies the process faults utilizing the correlation information but cannot accurately
estimate the variance since SSBL assumes the stationary process faults over KPC samples. The performance of UGSBL, MSBL, and [10] represent similar trends to the performance of AUC.
